Еще в 20-х гг. А. Лотка, а несколько позднее независимо от него В.Вольтера предложили математические модели, описывающие сопряженные колебания численности хищника и жертвы.
Модель состоит из двух компонентов:
С – численность хищников; N – численность жертв;
Предположим, что в отсутствии хищников популяция жертвы будет расти экспоненциально: dN/dt = rN. Но жертвы уничтожаются хищниками со скоростью, которая определяется частотой встреч хищника с жертвой, а частота встреч возрастает по мере увеличения численности хищника (С) и жертвы (N). Точное число встреченных и успешно съеденных жертв будет зависеть от эффективности, с которой хищник находит и ловит жертву, т.е. от а’ – «эффективности поиска» или «частоты нападений». Т.о., частота «успешных» встреч хищника с жертвой и, следовательно, скорость поедания жертв будет равна а’СN и в целом: dN/dt = rN – a’CN (1*).
В отсутствии пищи отдельные особи хищника теряют в весе, голодают и гибнут. Предположим, что в рассматриваемой модели численность популяции хищника в отсутствии пищи вследствие голодания будет уменьшаться экспоненциально: dC/dt = - qC, где q – смертность. Гибель компенсируется рождением новых особей со скоростью, которая, как полагают в этой модели, зависит от двух обстоятельств:
1) скорости потребления пищи, a’CN;
2)эффективности (f), с которой эта пища переходит в потомство хищника.
Т.о., рождаемость хищника равна fa’CN и в целом: dC/dt = fa’CN – qC (2*). Уравнения 1* и 2* составляют модель Лотки-Вольтера. Свойства этой модели можно исследовать, построить изоклины линии, соответствующие постоянной численности популяции, с помощью таких изоклин определяют поведение взаимодействующих популяций хищник-жертва.
В случае с популяцией жертвы: dN/dt = 0, rN = a’CN, или C = r/a’. Т.к. r и a’ = const, изоклиной для жертвы будет линия, для которой величина С является постоянной:
При низкой плотности хищника (С), численность жертвы (N) возрастает, наоборот – снижается.
Точно также для хищников (уравнение 2*) при dC/dt = 0, fa’CN = qC, или N = q/fa’, т.е. изоклиной для хищника будет линия, вдоль которой N постоянна: При высокой плотности жертвы, численность популяции хищника растет, а при низкой – снижается.
Их численность претерпевает неограниченные сопряженные колебания. Когда велико число жертв, численность хищников растет, что приводит к увеличению пресса хищников на популяцию жертвы и тем самым к уменьшению ее численности. Это снижение в свою очередь ведет к ограничению хищников в пище и падению их численности, которая вызывает ослабление пресса хищников и увеличение численности жертвы, что снова приводит к росту популяции хищников и т.д.
Популяции неограниченно долго совершают один и тот же цикл колебаний до тех пор, пока какое-либо внешнее воздействие не изменит их численность, после чего популяции совершают новые циклы неограниченных колебаний. На самом деле среда постоянно меняется, и численность популяций будет постоянно смещаться на новый уровень. Чтобы циклы колебаний, которые совершает популяция, были регулярными, они должны быть стабильными: если внешнее воздействие изменяет уровень численности популяций, то они должны стремиться к первоначальному циклу. Такие циклы называются устойчивыми, предельными циклами.
Модель Лотки-Вольтера позволяет показать основную тенденцию в отношениях хищник-жертва, которая выражается в возникновении колебаний численности в популяции жертвы, сопровождающихся колебаниями численности в популяции хищника. Основным механизмом таких колебаний является запаздывание во времени, свойственное последовательности состояния от высокой численности жертв к высокой численности хищников, затем к низкой численности жертв и низкой численности хищников, к высокой численности жертв и т.д.
5) ПОПУЛЯЦИОННЫЕ СТРАТЕГИИ ХИЩНИКА И ЖЕРТВЫ
Взаимоотношения «хищник - жертва» представляют звенья процесса передачи вещества и энергии от фитофагов к зоофагам или от хищников низшего порядка к хищникам высшего порядка. По характеру этих отношений различают три варианта хищников :
а) собиратели . Хищник собирает мелких достаточно многочисленных подвижных жертв. Такой вариант хищничества характерен для многих видов птиц (ржанок, зябликов, коньков и др.), которые затрачивают энергию только на поиск жертв;
б) истинные хищники . Хищник преследует и убивает жертву;
в) пастбищники . Эти хищники используют жертву многократно, например, оводы или слепни.
Стратегия добывания пищи у хищников направлена на обеспечение энергетической эффективности питания: затраты энергии на добывание пищи должны быть меньше энергии, получаемой при ее усвоении.
Истинные хищники делятся на
«жнецов», которые питаются обильными ресурсами (н, планктонные рыбы и даже усатый кит), и «охотников», которые добывают менее обильный корм. В свою очередь
«охотники» делятся на «засадников», подстерегающих добычу (например, щука, ястреб, кошка, жук- богомол), «искателей» (насекомоядные птицы) и «преследователей». Для последней группы поиск пищи не требует больших затрат энергии, но ее нужно много, чтобы овладеть жертвой (львы в саваннах). Впрочем, некоторые хищники могут сочетать элементы стратегии разных вариантов охоты.
Как и при отношениях «фитофаг - растение», ситуация, при которой все жертвы будут съедены хищниками, что в конечном итоге приведет и к их гибели, в природе не наблюдается. Экологическое равновесие между хищниками и жертвами поддерживается специальными механизмами , снижающими риск полного истребления жертв. Так, жертвы могут :
Убегать от хищника. В этом случае в результате адаптаций повышается подвижность и жертв, и хищников, что особенно характерно для степных животных, которым негде прятаться от преследователей;
Приобретать защитную окраску («притворяться» листьями или сучками) или, напротив, яркий цвет, Н.: красный, предупреждающий хищника о горьком вкусе. Общеизвестно изменение окраски зайца в разные времена года, что позволяет ему маскироваться летом в траве, а зимой на фоне белого снега. Адаптивное изменение окраски может происходить в разных стадиях онтогенеза: детеныши тюленей белые (цвет снега), а взрослые особи черные (цвет скалистого побережья);
Распространяться группами, что делает их поиск и промысел для хищника более энергоемким;
Прятаться в укрытия;
Переходить к мерам активной обороны (травоядные, имеющие рога, колючие рыбы), иногда совместной (овцебыки могут занимать «круговую оборону» от волков и т.д.).
В свою очередь хищники развивают не только способность к быстрому преследованию жертв, но и обоняние, позволяющее по запаху определить место нахождения жертвы. Многие виды хищников разрывают норы своих жертв (лисы, волки).
В то же время сами они делают все возможное для того, чтобы не обнаружить своего присутствия. Этим объясняется чистоплотность мелких кошачьих, которые для устранения запаха много времени тратят на туалет и закапывают экскременты. Хищники одевают «маскировочные халаты» (полосатость щук и окуней, делающих их менее заметными в зарослях макрофитов, полосатость тигров и т.д.).
Полной защиты от хищников всех особей в популяциях животных-жертв также не происходит, так как это привело бы не только к гибели голодающих хищников, но в конечном итоге - к катастрофе популяций жертв. В то же время при отсутствии или снижении плотности популяции хищников ухудшается генофонд популяции жертв (сохраняются больные и старые животные) и ввиду резкого увеличения их численности подрывается кормовая база.
По этой причине эффект зависимости численности популяций жертв и хищников - пульсация численности популяции жертвы, за которой с некоторым запаздыванием пульсирует численность популяции хищника («эффект Лотки - Вольтерры») - наблюдается редко.
Между биомассами хищников и жертв устанавливается достаточно устойчивое соотношение. Так, Р. Риклефс приводит данные о том, что соотношение биомасс хищника и жертвы колеблется в пределах 1:150 - 1:300. В разных экосистемах умеренной зоны США на одного волка приходится 300 мелких белохвостых оленей (вес 60 кг), 100 крупных оленей вапити (вес 300 кг) или 30 лосей (вес 350). Такая же закономерность выявлена в саваннах.
При интенсивной эксплуатации популяций фитофагов человек нередко исключает из экосистем хищников (в Великобритании, к примеру, есть косули и олени, но нет волков; в искусственных водоемах, где разводят карпа и другую прудовую рыбу, нет щук). В этом случае роль хищника выполняет сам человек, изымая часть особей популяции фитофага.
Особый вариант хищничества наблюдается у растений и грибов. В царстве растений встречается порядка 500 видов, способных ловить насекомых и частично их переваривать с помощью протеолитических ферментов. Хищные грибы образуют ловчие аппараты в виде маленьких овальных или шаровидных головок, расположенных на коротких веточках мицелия. Однако самый распространенный вид ловушки - клейкие трехмерные сети, состоящие из большого числа колец, образующихся в результате ветвления гиф. Хищные грибы могут ловить достаточно крупных животных, например, круглых червей. После того, как червь запутается в гифах, они прорастают внутрь тела животного и быстро его заполняют.
1.Постоянный и благоприятный уровень температуры и влажности.
2.Обилие пищи.
3.Защита от неблагоприятных факторов.
4.Агрессивный химический состав среды обитания (пищеварительные соки).
1.Наличие двух сред обитания: среда первого порядка - организм хозяина, среда второго порядка - внешняя среда.
Модели взаимодействия двух видов
Гипотезы Вольтерра. Аналогии с химической кинетикой. Вольтерровские модели взаимодействий. Классификация типов взаимодействий Конкуренция. Хищник-жертва. Обобщенные модели взаимодействия видов. Модель Колмогорова. Модель взаимодействия двух видов насекомых Макартура. Параметрический и фазовые портреты системы Базыкина.
Основателемсовременной математической теории популяций справедливо считается итальянский математик Вито Вольтерра, разработавший математическую теорию биологических сообществ, аппаратом которой служат дифференциальные и интегро-дифференциальные уравнения. (Vito Volterra. Lecons sur la Theorie Mathematique de la Lutte pour la Vie. Paris , 1931). В последующие десятилетия популяционная динамика развивалась, в основном, в русле высказанных в этой книге идей. Русский перевод книги Вольтерра вышел в 1976 г. под названием: «Математическая теория борьбы за существование» с послесловием Ю.М. Свирежева, в котором рассматривается история развития математической экологии в период 1931‑1976 гг.
Книга Вольтерра написана так, как пишут книги по математике. В ней сначала сформулированы некоторые предположения о математических объектах, которые предполагается изучать, а затем проводится математическое исследование свойств этих объектов.
Системы, изученные Вольтерра, состоят их двух или нескольких видов. В отдельных случаях рассматривается запас используемой пищи. В основу уравнений, описывающих взаимодействие этих видов, положены следующие представления.
Гипотезы Вольтерра
1. Пища либо имеется в неограниченном количестве, либо ее поступление с течением времени жестко регламентировано.
2. Особи каждого вида отмирают так, что в единицу времени погибает постоянная доля существующих особей.
3. Хищные виды поедают жертв, причем в единицу времени количество съеденных жертв всегда пропорционально вероятности встречи особей этих двух видов, т.е. произведению количества хищников на количество жертв.
4. Если имеется пища в ограниченном количестве и несколько видов, которые способны ее потреблять, то доля пищи, потребляемой видом в единицу времени, пропорциональна количеству особей этого вида, взятому с некоторым коэффициентом, зависящим от вида (модели межвидовой конкуренции).
5. Если вид питается пищей, имеющейся в неограниченном количестве, прирост численности вида в единицу времени пропорционален численности вида.
6. Если вид питается пищей, имеющейся в ограниченном количестве, то его размножение регулируется скоростью потребления пищи, т.е. за единицу времени прирост пропорционален количеству съеденной пищи.
Аналогии с химической кинетикой
Эти гипотезы имеют близкие параллели с химической кинетикой. В уравнениях популяционной динамики, как и в уравнениях химической кинетики, используется “принцип соударений”, когда скорость реакции пропорциональна произведению концентраций реагирующих компонентов.
Действительно, согласно гипотезам Вольтерра, скорость процесса отмирания каждого вида пропорциональна численности вида. В химической кинетике это соответствует мономолекулярной реакции распада некоторого вещества, а в математической модели – отрицательным линейным членам в правых частях уравнений.
Согласно представлениям химической кинетики, скорость бимолекулярной реакции взаимодействия двух веществ пропорциональна вероятности столкновения этих веществ, т.е. произведению их концентрации. Точно так же, в соответствии с гипотезами Вольтерра, скорость размножения хищников (гибели жертв) пропорциональна вероятности встреч особей хищника и жертвы, т.е. произведению их численностей. И в том и в другом случае в модельной системе появляются билинейные члены в правых частях соответствующих уравнений.
Наконец, линейные положительные члены в правых частях уравнений Вольтерра, отвечающие росту популяций в неограниченных условиях, соответствуют автокаталитическим членам химических реакций. Такое сходство уравнений в химических и экологических моделях позволяет применить для математического моделирования кинетики популяций те же методы исследований, что и для систем химических реакций.
Классификация типов взаимодействий
В соответствии с гипотезами Вольтерра взаимодействие двух видов, численности которых x 1 иx 2 , могут быть описаны уравнениями:
(9.1)
Здесь параметры a i ‑ константы собственной скорости роста видов, c i ‑ константы самоограничения численности (внутривидовой конкуренции), b ij ‑ константы взаимодействия видов, (i , j= 1,2). Знаки этих коэффициентов определяют тип взаимодействия.
В биологической литературе обычно классифицируют взаимодействия по участвующим в них механизмам. Разнообразие здесь огромно: различные трофические взаимодействия, химические взаимодействия, существующие между бактериями и планктонными водорослями, взаимодействия грибов с другими организмами, сукцессии растительных организмов, связанные в частности, с конкуренцией за солнечный свет и с эволюцией почв и т.д. Такая классификация кажется необозримой.
E . Одум, учитывая предложенные В.Вольтерра модели, предложил классификацию не по механизмам, а по результатам. Согласно этой классификации, оценивать взаимоотношения следует как положительные, отрицательные или нейтральные в зависимости от того, возрастает, убывает или остается неизменной численность одного вида в присутствии другого вида. Тогда основные типы взаимодействий могут быть представлены в виде таблицы.
ТИПЫ ВЗАИМОДЕЙСТВИЯ ВИДОВ
|
СИМБИОЗ |
b 12 ,b 21 >0 |
||
|
КОММЕНСАЛИЗМ |
b 12 ,>0, b 21 =0 |
||
|
ХИЩНИК-ЖЕРТВА |
b 12 ,>0, b 21 <0 |
||
|
АМЕНСАЛИЗМ |
b 12 ,=0, b 21 <0 |
||
|
КОНКУРЕНЦИЯ |
b 12 , b 21 <0 |
||
|
НЕЙТРАЛИЗМ |
b 12 , b 21 =0 |
В последнем столбце указаны знаки коэффициентов взаимодействия из системы (9.1)
Рассмотрим основные типы взаимодействий
УравненияКОНКУРЕНЦИИ:
Как мы уже видели в лекции 6, уравнения конкуренции имеют вид:
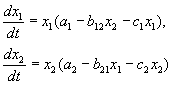 (9.2)
(9.2)
Стационарные решения системы:
(1).
![]()
Начало координат, при любых параметрах системы представляет собой неустойчивый узел.
(2).
![]() (9.3)
(9.3)
C тационарное состояние (9.3) представляет собой седло при a 1 >b 12 /с 2 и
устойчивый узел приa 1 12 /с 2 . Это условие означает, что вид вымирает, если его собственная скорость роста меньше некоторой критической величины.
(3).
![]() (9.4)
(9.4)
C тационарное решение (9.4) ¾ седло при a 2 >b 21 /c 1 и устойчивый узел при a 2< b 21 /c 1
(4).
![]() (9.5)
(9.5)
Стационарное состояние (9.5) характеризует сосуществование двух конкурирующих видов и представляет собой устойчивый узел в случае выполнения соотношения:
![]()
Отсюда следует неравенство:
b
12
b
21
позволяющее сформулировать условие сосуществования видов:
Произведение коэффициентов межпопуляционного взаимодействия меньше произведения коэффициентов внутри популяционного взаимодействия.
Действительно, пусть естественные скорости роста двух рассматриваемых видов a 1 , a 2 одинаковы. Тогда необходимым для устойчивости условием будет
c 2 > b 12 ,c 1 > b 21 .
Эти неравенства показывают, что увеличение численности одного из конкурентов сильнее подавляет его собственный рост, чем рост другого конкурента. Если численность обоих видов ограничивается, частично или полностью, различными ресурсами, приведенные выше неравенства справедливы. Если же оба вида имеют совершенно одинаковые потребности, то один из них окажется более жизнеспособным и вытеснит своего конкурента.
Поведение фазовых траекторий системы дает наглядное представление о возможных исходах конкуренции. Приравняем нулю правые части уравнений системы (9.2):
x 1 (a 1 –c 1 x 1 – b 12 x 2) = 0 (dx 1 /dt = 0),
x 2 (a 2 –b 21 x 1 – c 2 x 2) = 0 (dx 2 /dt = 0),
При этом получим уравнения для главных изоклин системы
x 2 = – b 21 x 1 / c 2 +a 2 /c 2 , x 2 = 0
– уравнения изоклин вертикальных касательных.
x 2 = – c 1 x 1 / b 12 +a 1 /b 12 , x 1 = 0
– уравнения изоклин вертикальных касательных.
Точки попарного пересечения изоклин вертикальных и горизонтальных касательных
систем представляют собой стационарные решения системы уравнений (9.2.), а их
координаты ![]() суть стационарные численности конкурирующих видов.
суть стационарные численности конкурирующих видов.
Возможное расположение главных изоклин в системе (9.2) изображено на рис.9.1. Рис. 9.1 а соответствует выживанию вида x 1 , рис. 9.1 б – выживанию вида x 2 , рис. 9.1 в – сосуществованию видов при выполнении условия (9.6). Рисунок 9.1 г демонстрирует триггерную систему. Здесь исход конкуренции зависит от начальных условий. Ненулевое для обоих видов стационарное состояние (9.5) – неустойчивое. Это – седло, через которое проходит сепаратриса, отделяющая области выживания каждого из видов.

Рис. 9.1. Расположение главных изоклин на фазовом портрете вольтерровской системы конкуренции двух видов (9.2) при разном соотношении параметров. Пояснения в тексте.
Для изучения конкуренции видов ставились эксперименты на самых различных организмах. Обычно выбирают два близкородственных вида и выращивают их вместе и по отдельности в строго контролируемых условиях. Через определенные промежутки времени проводят полный или выборочный учет численности популяции. Регистрируют данные по нескольким повторным экспериментам и анализируют. Исследования проводили на простейших (в частности, инфузориях), многих видах жуков рода Tribolium, дрозофиллах, пресноводных ракообразных (дафниях). Много экспериментов проводилось на микробных популяциях (см. лекция 11). В природе также проводили эксперименты, в том числена планариях (Рейнольдс), двух видах муравьев (Понтин) и др. На рис. 9.2. изображены кривые роста диатомовых водорослей, использующих один и тот же ресурс (занимающих одну и ту же экологическую нишу). При выращивании в монокультуре Asterionella Formosa выходит на постоянный уровень плотности и поддержвает концентрацию ресурса (силиката) на постоянно низком уровне. Б. При выращивании в монокультуре Synedrauina ведет себя сходным образом и поддерживает концентрацию силиката на еще более низком уровне. В. При совместном культивировании (в двух повторностях) Synedrauina вытесняет Asterionella Formosa . По-видимому, Synedra

Рис. 9.2. Конкуренция у диатомовых водорослей. а ‑ при выращивании в монокультуре Asterionella Formosa выходит на постоянный уровень плотности и поддерживает концентрацию ресурса (силиката) на постоянно низком уровне.б ‑ при выращивании в монокультуре Synedrauina ведет себя сходным образом и поддерживает концентрацию силиката на еще более низком уровне. в ‑ при совместном культивировании (в двух повторностях) Synedruina вытесняет Asterionella Formosa . По-видимому, Synedra выигрывает конкуренцию благодаря своей способности к более полному использованию субстрата (см. также Лекцию 11).
Широко известны эксперименты по изучению конкуренции Г. Гаузе, продемонстрировавшие выживание одного из конкурирующих видов и позволившие ему сформулировать «закон конкурентного исключения». Закон гласит, что в одной экологической нише может существовать только один вид. На рис. 9.3. приведены результаты экспериментов Гаузе для двух видов Parametium , занимающих одну экологическую нишу (рис. 9.3 а, б) и видами, занимающими разные экологические ниши (рис. 9.3. в).

Рис. 9.3. а - Кривые роста популяций двух видов Parametium в одновидовыхкультурах. Черные кружки – P Aurelia , белые кружки – P . Caudatum
б - Кривые роста P Aurelia и P . Caudatum в смешанной культуре.
По Gause , 1934
Модель конкуренции (9.2) имеет недостатки, в частности, из нее следует, что сосуществование двух видов возможно лишь в случае, если их численность ограничивается разными факторами, но модель не дает указаний, насколько велики должны быть различия для обеспечения длительного сосуществования. В то же время известно, что для длительного сосуществования в изменчивой среде необходимо различие, достигающее определенной величины. Внесение в модель стохастических элементов (например, введение функции использования ресурса) позволяет количественно исследовать эти вопросы.
Система ХИЩНИК+ЖЕРТВА
 (9.7)
(9.7)
Здесь, в отличие от (9.2) знаки b 12 и b 21 - разные. Как и в случае конкуренции, начало координат
![]() (9.8)
(9.8)
является особой точкой типа неустойчивый узел. Три других возможных стационарных состояния:
![]() ,(9.9)
,(9.9)
![]() (9.10)
(9.10)
![]() (9.11)
(9.11)
Таким образом, возможно выживание только жертвы (9.10), только хищника (9.9) (если у него имеются и другие источники питания) и сосуществование обоих видов (9.11). Последний вариант уже был рассмотрен нами в лекции 5. Возможные типы фазовых портретов для системы хищник-жертва представлены на рис. 9.4.
Изоклины горизонтальных касательных представляют собой прямые
x 2 = – b 21 х 1 /c 2 + a 1 /c 2 , х 2 = 0,
а изоклины вертикальных касательных – прямые
x 2 = – c 1 х 1 /b 12 + a 2 /b 12 , х 1 = 0.
Стационарные точки лежат на пересечении изоклин вертикальных и горизонтальных касательных.

Из рис. 9.4 видно следующее. Система хищник – жертва (9.7) может иметь устойчивое положение равновесия, в кот o ром популяция жертв полностью вымерла ( ) и остались только хищники (точка 2 на рис. 9.4 а). Очевидно, такая ситуация может реализоваться лишь в случае, если кроме рассматриваемого вида жертв х 1 хищник х 2 – имеет дополнительные источники питания. Этот факт в модели отражается положительным членом в правой части уравнения для х 2 . Особые точки (1) и (3) (рис. 9.4 а ) являются неустойчивыми. Вторая возможность – устойчивое стационарное состояние, в котором популяция хищников полностью вымерла и остались одни жертвы – устойчивая точка (3) (рис. 9.4 6 ). Здесь особая точка (1) – также неустойчивый узел.
Наконец, третья возможность – устойчивое сосуществование популяций хищника и жертвы (рис. 9.4 в ), стационарные численности которых выражаются формулами (9.11).
Как и в случае одной популяции (см. Лекция 3), для модели (9.7) можно разработать стохастическую модель, но для нее нельзя получить решение в явном виде. Поэтому мы ограничимся общими рассуждениями. Допустим, например, что точка равновесия находится на некотором расстоянии от каждой из осей. Тогда для фазовых траекторий, на которых значения x 1 , x 2 остаются достаточно большими, вполне удовлетворительной будет детерминистическая модель. Но если в некоторой точке фазовой траектории какая–либо переменная не очень велика, то существенное значение могут приобрести случайные флюктуации. Они приводят к тому, что изображающая точка переместится на одну из осей, что означает вымирание соответствующего вида.
Таким образом, стохастическая модель оказывается неустойчивой, так как стохастический “дрейф” рано или поздно приводит к вымиранию одного из видов. В такого рода модели хищник в конечном счете вымирает, это может произойти либо случайно, либо вследствие того, что сначала элиминируется популяция его жертвы. Стохастическая модель системы хищник – жертва хорошо объясняет эксперименты Гаузе (Гаузе, 1934), в которых инфузория Paramettum candatum служила жертвой для другой инфузории Didinium nasatum – хищника. Ожидавшиеся согласно детерминистическим уравнениям (9.7) равновесные численности в этих экспериментах составляли примерно всего по пять особей каждого вида, так что нет ничего удивительного в том, что в каждом повторном эксперименте довольно быстро вымирали либо хищники, либо жертвы (а за ними и хищники) Результаты экспериментов представлены на рис. 9.5.

Рис . 9.5. Рост Parametium caudatum и хищной инфузории Dadinium nasutum . Из : Gause G.F. The struggle for existence. Baltimore , 1934
Итак, анализ вольтерровских моделей взаимодействия видов показывает, что, несмотря на большое разнообразие типов поведения таких систем, незатухающих колебаний численности в модели конкурирующих видов не может быть вовсе. Однако в природе и в эксперименте такие колебания наблюдаются. Необходимость их теоретического объяснения послужила одной из причин для формулировки модельных описаний в более общем виде.
Обобщенные модели взаимодействия двух видов
Было предложено большое число моделей, описывающих взаимодействие видов, правые части уравнений которых представляли собой функции численностей взаимодействующих популяций. Решался вопрос о выработке общих критериев, позволяющих установить, какого вида функции могут описать особенности поведения временного численности популяции, в том числе устойчивые колебания. Наиболее известные из этих моделей принадлежат Колмогорову (1935, переработанная статья ‑ 1972) и Розенцвейгу (1963).
 (9.12)
(9.12)
В модель заложены следующие предположения:
1) Хищники не взаимодействуют друг с другом, т.е. коэффициент размножения хищников k 2 и число жертв L , истребляемых в единицу времени одним хищником, не зависит от y.
2) Прирост числа жертв при наличии хищников равен приросту в отсутствие хищников минус число жертв, истребляемых хищниками. Функции k 1 (x ), k 2 (x ), L (x ), ‑ непрерывны и определены на положительной полуоси x , y ³ 0.
3) dk 1 /dx< 0. Это означает, что коэффициент размножения жертв в отсутствие хищника монотонно убывает с возрастанием численности жертв, что отражает ограниченность пищевых и иных ресурсов.
4) dk 2 / dx> 0, k 2 (0) < 0 < k 2 (¥ ). С ростом численности жертв коэффициент размножения хищников монотонно убывает с возрастанием численности жертв, переходя от отрицательных значений, (когда нечего есть) к положительным.
5) Число жертв, истребляемых одним хищником в единицу времени L (x )> 0 при N> 0; L (0)=0.
Возможные типы фазовых портретов системы (9.12) представлены на рис. 9.6:

Рис. 9.6. Фазовые портреты системы Колмогорова (9.12), описывающей взаимодействие двух видов при разных соотношениях параметров. Пояснения в тексте.
Стационарные решения (их два или три) имеют следующие координаты:
(1). ` x=0; ` y=0 .
Начало координат при любых значениях параметров представляет собой седло(рис. 9.6 а-г).
(2). ` x=A, ` y=0. (9.13)
A определяется из уравнения:
k 1 (A )=0.
Стационарное решение (9.13) ‑ седло, если B< A (рис. 9.6 а , б , г ), B определяется из уравнения
k 2 (B )=0
Точка (9.13) помещается в положительном квадранте, еслиB>A. Это ‑ устойчивый узел.
Последний случай, который соответствует гибели хищника и выживанию жертвы,представлен на рис. 9.6 в .
(3). ` x=B, ` y=C. (9.14)
Величина С определяется из уравнений:
Точка (9.14) – фокус (рис.9.6 а ) или узел (рис.9.6 г ), устойчивость которых зависит от знакавеличины s
s 2 = – k 1 (B) – k 1 (B )B+L (B )C.
Если s >0, точка устойчива, если s <0 ‑ точка неустойчива, и вокруг нее могут существовать предельные циклы (рис. 9.6 б )
В зарубежной литературе чаще рассматривается сходная модель, предложенная Розенцвейгом и Макартуром (1963):
 (9.15)
(9.15)
где f (x ) - скорость изменения численности жертв x в отсутствие хищников, Ф(x,y ) ‑ интенсивность хищничества, k ‑ коэффициент, характеризующий эффективность переработки биомассы жертвы в биомассу хищника, e - смертность хищника.
Модель (9.15) сводится к частному случаю модели Колмогорова (9.12) при следующих предположениях:
1) численность хищника ограничивается только численностью жертвы,
2) скорость, с которой данная особь хищника поедает жертву, зависит только от плотности популяции жертв и не зависит от плотности популяции хищников.
Тогда уравнения (9.15) принимают вид.

При описании взаимодействия реальных видов, правые части уравнений конкретизируются в соответствии с представлениями о биологических реалиях. Рассмотрим одну из самых популярных моделей такого типа.
Модельвзаимодействиядвух видов насекомых (M acArthur, 1971)
Модель, которую мы рассмотрим ниже, использовалась для решения практической задачи борьбы с вредными насекомыми с помощью стерилизации самцов одного из видов. Исходя из биологических особенностей взаимодействия видов, была написана следующая модель
 (9.16)
(9.16)
Здесь x,y - биомассы двух видов насекомых. Трофические взаимодействия описываемых в этой модели видов – весьма сложные. Этим определяется вид многочленов в правых частях уравнений.
Рассмотрим правую часть первого уравнения. Насекомые вида х поедают личинок вида у (член + k 3 y), но взрослые особи вида у поедают личинок вида х при условии высокой численности видов х или у или обоих видов (члены – k 4 xy, – у 2 ). При малых х смертность вида х выше, чем его естественный прирост (1–k 1 +k 2 x–x 2 < 0 при малых х). Во втором уравнении член k 5 отражает естественный прирост вида y; –k 6 y – самоограничение этого вида, –k 7 x – поедание личинок вида у насекомыми вида х, k 8 xy – прирост биомассы вида у за счет поедания взрослыми насекомыми вида у личинок вида х.
На рис. 9.7 представлен предельный цикл, являющийся траекторией устойчивого периодического решения системы (9.16).

Решение вопроса о том, каким образом обеспечить сосуществование популяции с ее биологическим окружением, разумеется, не может быть получено без учета специфики конкретной биологической системы и анализа всех ее взаимосвязей. Вместе с тем изучение формальных математических моделей позволяет ответить на некоторые общие вопросы. Можно утверждать, что для моделей типа (9.12) факт совместимости или несовместимости популяций не зависит от их начальной численности, а определяется только характером взаимодействия видов. Модель помогает ответить на вопрос: как следует воздействовать на биоценоз, управлять им, чтобы по возможности быстро уничтожить вредный вид.
Управление может сводиться к кратковременному, скачкообразному изменению величин численности х и у. Такой способ отвечает методам борьбы типа однократного уничтожения одной или обеих популяций химическими средствами. Из сформулированного выше утверждения видно, что для совместимых популяций этот метод борьбы будет малоэффективным, поскольку с течением времени система опять выйдет на стационарный режим.
Другой способ ‑ изменение вида функций взаимодействия между видами, например, при изменении значений параметров системы. Именно такому, параметрическому, способу отвечают биологические методы борьбы. Так при внедрении стерилизованных самцов уменьшается коэффициент естественного прироста популяции. Если при этом мы получим другой тип фазового портрета, такой, где имеется лишь устойчивое стационарное состояние с нулевой численностью вредителя, управление приведет к желаемому результату – уничтожению популяции вредного вида. Интересно отметить, что иногда воздействие целесообразно применить не к самому вредителю, а к его партнеру. Какой из способов более эффективен, в общем случае сказать нельзя. Это зависит от имеющихся в распоряжении средств управления и от явного вида функций, описывающих взаимодействие популяций.
Модель А.Д.Базыкина
Теоретический анализ моделей взаимодействий видов наиболее исчерпывающе проведен в книге А.Д.Базыкина “Биофизика взаимодействующих популяций” (М., Наука, 1985).
Рассмотрим одну из изученных в этой книге моделей типа хищник-жертва.
 (9.17)
(9.17)
Система (9.17) является обобщением простейшей модели хищник-жертва Вольтерра (5.17) с учетом эффекта насыщения хищников. В модели (5.17) предполагается, что интенсивность выедания жертв линейно растет с ростом плотности жертв, что при больших плотностях жертв не соответствует реальности. Для описания зависимости рациона хищника от плотности жертв могут быть выбраны разные функции. Наиболее существенно, чтобы выбранная функция с ростом x асимптотически стремилась к постоянному значению. В модели (9.6) использовалась логистическая зависимость. В модели Базыкина в роли такой функции выбрана гипербола x /(1+px ). Вспомним, что такой вид имеет формула Моно, описывающая зависимость скорость роста микроорганизмов от концентрации субстрата. Здесь в роли субстрата выступает жертва, а в роли микроорганизмов – хищник.
Система (9.17) зависит от семи параметров. Число параметров можно уменьшить с помощью замены переменных:
x ® (A/D )x; y ® (A/D )/y;
t ® (1/A )t; g (9.18)
и зависит от четырех параметров.
Для полного качественного исследования необходимо разбить четырехмерное пространство параметров на области с различным типом динамического поведения, т.е. построить параметрический, или структурный портрет системы.
Затем надо построить фазовые портреты для каждой из областей параметрического портрета и описать бифуркации, происходящие с фазовыми портретами на границах различных областей параметрического портрета.
Построение полного параметрического портрета производится в виде набора “срезов” (проекций) параметрического портрета малой размерности при фиксированных значениях некоторых из параметров.
Параметрический портрет системы (9.18) при фиксированных g и малых e представлен на рис.9.8. Портрет содержит 10 областей с различным типом поведения фазовых траекторий.

Рис. 9.8. Параметрический портрет системы (9.18) при фиксированных g
и малых e
Поведение системы при различных соотношениях параметров может быть существенно различным (рис.9.9). В системе возможны:
1) одно устойчивое равновесие (области 1 и 5);
2) один устойчивый предельный цикл (области 3 и 8);
3) два устойчивых равновесия (область 2)
4) устойчивый предельный цикл и неустойчивое равновесие внутри него (области 6, 7, 9, 10)
5) устойчивый предельный цикл и устойчивое равновесие вне его (область 4).
В параметрических областях 7, 9, 10 область притяжения равновесия ограничивается неустойчивым предельным циклом, лежащим внутри устойчивого. Наиболее интересно устроен фазовый портрет, соответствующий области 6 на параметрическом портрете. Детально он изображен на рис. 9.10.

Область притяжения равновесия В 2 (заштрихована) представляет собой “улитку”, скручивающуюся с неустойчивого фокуса В 1 . Если известно, что в начальный момент времени система находилась в окрестности В 1 , то судить о том, придет ли соответствующая траектория в равновесие В 2 или на устойчивый предельный цикл, окружающий три точки равновесия С (седло), В 1 и В 2 можно лишь на основе вероятностных соображений.

Рис.9.10. Фазовый портрет системы 9.18 для параметрической области 6. Область притяжения В 2 заштрихована
На параметрическом портрете (9.7) имеются 22 различные бифуркационные границы, которые образуют 7 различных типов бифуркаций. Их изучение позволяет выявить возможные типы поведения системы при изменении ее параметров. Например, при переходе из области 1 в область 3 происходит рождение малого предельного цикла, или мягкое рождение автоколебаний вокруг единственного равновесия В. Аналогичное мягкое рождение автоколебаний, но вокруг одного из равновесий, а именно B 1 , происходит при пересечении границы областей 2 и 4. При переходе из области 4 в область 5 устойчивый предельный цикл вокруг точки B 1 “лопается” на петле сепаратрис и единственной притягивающей точкой остается равновесие B 2 и т.д.
Особый интерес для практики представляет, конечно, выработка критериев близости системы к бифуркационным границам. Действительно, биологам хорошо известно свойство “буферности”, или “гибкости”, природных экологических систем. Этими терминами обычно обозначают способность системы как бы поглощать внешние воздействия. Пока интенсивность внешнего воздействия не превышает некоторой критической величины, поведение системы не претерпевает качественных изменений. На фазовой плоскости это соответствует возвращению системы в устойчивое состояние равновесия или на устойчивый предельный цикл, параметры которого не сильно отличаются от первоначального. Когда же интенсивность воздействия превышает допустимую, система “ломается”, переходит в качественно иной режим динамического поведения, например просто вымирает. Это явление соответствует бифуркационному переходу.
Каждый тип бифуркационных переходов имеет свои отличительные особенности, позволяющие судить об опасности такого перехода для экосистемы. Приведем некоторые общие критерии, свидетельствующие о близости опасной границы. Как и в случае одного вида, если при уменьшении численности одного из видов происходит “застревание” системы вблизи неустойчивой седловой точки, что выражается в очень медленном восстановлении численности к начальному значению, значит, система находится вблизи критической границы. Индикатором опасности служит также изменение формы колебаний численностей хищника и жертвы. Если из близких к гармоническим колебания становятся релаксационными, причем амплитуда колебаний увеличивается, это может привести к потере устойчивости системы и вымиранию одного из видов.
Дальнейшее углубление математической теории взаимодействия видов идет по линии детализации структуры самих популяций и учета временных и пространственных факторов.
Литература.
Колмогоров А.Н. Качественное изучение математических моделей динамики популяций. // Пороблемы кибернетики. М ., 1972, Вып .5.
MacArtur R. Graphycal analysis of ecological systems// Division of biology report Perinceton University. 1971
А.Д.Базыкин “Биофизика взаимодействующих популяций”. М., Наука, 1985.
В.Вольтерра: «Математическая теория борьбы за существование». М .. Наука , 1976
Gause G.F. The struggle for existence. Baltimore, 1934.
Модель «хищник - жертва» и макроэкономическая модель Гудвина
Рассмотрим биологическую модель «хищник - жертва», в которой один вид является кормом для другого. Эта модель, давно ставшая классической, была построена в первой половине XX в. итальянским математиком В. Вольтерра для объяснения колебаний уловов рыбы в Адриатическом море . В модели предполагается, что число хищников растет до тех пор, пока у них будет достаточно пищи, а увеличение поголовья хищников приводит к уменьшению популяции рыб-жертв. Когда последних становится мало, численность хищников уменьшается. Вследствие этого с некоторого момента начинается рост численности рыб-жертв, который через некоторое время вызывает рост популяции хищников. Цикл замыкается.
Пусть N x (t) и N 2 (t) - численности рыб-жертв и рыб-хищников в момент времени t соответственно. Предположим, что темп прироста численности жертв в условиях отсутствия хищников постоянен, т. е.
где а - положительная постоянная.
Появление хищника должно снизить темп прироста жертв. Будем считать, что это снижение линейно зависит от численности хищника: чем больше хищников, тем меньше темп прироста жертв. Тогда

где т > 0.
Поэтому для динамики численности рыб-жертв получаем:
Составим теперь уравнение, определяющее динамику популяции хищников. Предположим, что их численность в случае отсутствия жертв сокращается (из-за отсутствия корма) с постоянным темпом Ь, т. е.
![]()
Наличие жертв вызывает увеличение темпа прироста хищников. Предположим, что этот прирост линеен, т. е.
![]()
где п> 0.
Тогда для скорости роста рыб-хищников получаем уравнение:
В системе «хищник - жертва» (6.17)-(6.18) снижение скорости роста численности рыб-жертв, вызванное поеданием их хищниками, равно mN x N 2 , т. е. пропорционально числу их встреч с хищником. Увеличение скорости роста численности рыб-хищников, вызванное наличием жертв, равно nN x N 2 , т. е. тоже пропорционально числу встреч жертв и хищников.
Введем безразмерные переменные U = mN 2 /a и V = nN x /b. Динамика переменной U соответствует динамике хищников, а динамика переменной V - динамике жертв. В силу уравнений (6.17) и (6.18) изменение новых переменных определяется системой уравнений:
Предположим, что при t = 0 число особей обоих видов известно, следовательно, известны начальные значения новых переменных?/(0) = U 0 , К(0) = К 0 . Из системы уравнений (6.19) можно найти дифференциальное уравнение для ее фазовых траекторий:

Разделяя переменные этого уравнения, получим:


Рис. 6.10. Построение фазовой траектории ADCBA системы дифференциальных уравнений (6.19)
Отсюда с учетом начальных данных следует:
где константа интегрирования С = b(V Q - InV 0)/a - lnU 0 + U 0 .
На рис. 6.10 показано, как строится линия (6.20) при заданном значении С. Для этого в первой, во второй и в третьей четвертях соответственно строим графики функций х = V - InV, у = (Ь/а)х , у = = InU- U+C.
В силу равенства dx/dV = (V- 1)/У функция х = V- In К, определенная при V > 0, возрастает, если V> 1, и убывает, если V 1. В силу того, что cPx/dV 1 = 1/F 2 > 0, график функции л: = x(V) направлен выпуклостью вниз. Уравнение V= 0 задает вертикальную асимптоту. Наклонных асимптот эта функция не имеет. Поэтому график функции х = х(У) имеет вид кривой, изображенной в первой четверти рис. 6.10.
Аналогичным образом исследуется функция у = InU - U+ С, график которой на рис. 6.10 изображен в третьей четверти.
Если теперь мы разместим на рис. 6.10 во второй четверти график функции у = (Ь/а)х , то в четвертой четверти получим линию, которая связывает переменные U и V. Действительно, взяв точку V t на оси OV, вычисляем с помощью функции х = V - V соответствующее знание х х. После этого, используя функцию у = (Ь/а)х , по полученному значению х { находим у х (вторая четверть на рис. 6.10). Далее с помощью графика функции у = InU - U + С определяем соответствующие значения переменной U (на рис. 6.10 таких значений два - координаты точек М и N). Совокупность всех таких точек (V; U) образует искомую кривую. Из построения следует, что графиком зависимости (6.19) является замкнутая линия, содержащая внутри себя точку Е( 1, 1).
Напомним, что эту кривую мы получили, задав некоторые начальные значения U 0 и V 0 и вычислив по ним константу С. Взяв другие начальные значения, мы получим другую замкнутую линию, не пересекающую первую и также содержащую внутри себя точку Е( 1, 1). Это означает, что семейством траекторий системы (6.19) на фазовой плоскости (V, U) является множество замкнутых непересекающихся линий, концентрирующихся вокруг точки Е( 1, 1), а решения исходной модели U = Щ) и V = V{t) являются функциями, периодическими во времени. При этом максимум функции U = U(t) не попадает на максимум функции V = V(t ) и наоборот, т. е. колебания численности популяций около своих равновесных решений происходят в разных фазах.
На рис. 6.11 приведены четыре траектории системы дифференциальных уравнений (6.19) на фазовой плоскости OUV, отличающиеся начальными условиями. Одна из траекторий равновесная - это точка Е( 1, 1), которой соответствует решение U(t) = 1, V{t) = 1. Точки (U(t), V(t)) на других трех фазовых траекториях по мере увеличения времени смещаются по часовой стрелке.
Чтобы пояснить действие механизма изменения численности двух популяций, рассмотрим траекторию ABCDA на рис. 6.11. Как видим, на участке АВ и хищников, и жертв мало. Поэтому здесь популяция хищников сокращается из-за недостатка корма, а популяция жертв растет. На участке ВС численность жертв достигает высоких значений, что приводит к росту численности хищников. На участке СА хищников много, и это влечет сокращение численности жертв. При этом после прохождения точки D численность жертв уменьшается на столько, что численность популяции начинает уменьшаться. Цикл замыкается.
Модель «хищник - жертва» - пример структурно неустойчивой модели. Здесь малое изменение правой части одного из уравнений может привести к принципиальному изменению ее фазового портрета.

Рис. 6.11.

Рис. 6.12.
Действительно, если в уравнении динамики жертв учесть внутривидовую конкуренцию, то мы получим систему дифференциальных уравнений:
Здесь при т = 0 популяция жертв развивается согласно логическому закону.
При т Ф 0 ненулевое равновесное решение системы (6.21) при некоторых положительных значениях параметра внутривидовой конкуренции И является устойчивым фокусом, и соответствующие траектории «наматываются» на точку равновесия (рис. 6.12). Если же h = 0, то в этом случае особая точка Е( 1, 1) системы (6.19) является центром, и траектории представляют собой замкнутые линии (см. рис. 6.11).
Замечание. Обычно под моделью «хищник - жертва» понимают модель (6.19), фазовые траектории которой замкнуты. Однако модель (6.21) также является моделью «хищник - жертва», поскольку описывает взаимовлияние хищников и жертв.
Одним из первых приложений модели типа «хищник - жертва» в экономике для исследования циклично изменяющихся процессов является макроэкономическая модель Гудвина, в которой используется непрерывный подход к анализу взаимовлияния уровня занятости и ставки заработной платы.
В работе В.-Б. Занга изложен вариант модели Гудвина, в котором производительность труда и предложение труда растут с постоянными темпами прироста, а коэффициент выбытия фондов равен нулю. Эта модель формально приводит к уравнениям модели «хищник - жертва».
Ниже рассматривается модификация этой модели для случая отличного от нуля коэффициента выбытия фондов.
В модели используются следующие обозначения: L - численность трудящихся; w - средняя ставка заработной платы трудящихся; К - основные производственные фонды (капитал); Y - национальный доход; / - инвестиции; С - потребление; р - коэффициент выбытия фондов; N - предложение труда на рынке рабочей силы; т = Y/K - фондоотдача; а = Y/L - производительность труда; у = L/N - коэффициент занятости; х = C/Y - норма потребления в национальном доходе; К - приращение капитала в зависимости от инвестиций.
Выпишем уравнения модели Гудвина:

где а 0 , b, g, п, N 0 , г - положительные числа (параметры).
Уравнения (6.22) - (6.24) выражают следующее. Уравнение (6.22) - обычное уравнение динамики фондов. Уравнение (6.23) отражает рост ставки заработной платы при высоком уровне занятости (ставка заработной платы растет, если предложение труда невелико) и уменьшение ставки заработной платы при высоком уровне безработицы.
Тем самым уравнение (6.23) выражает закон Филлипса в линейной форме . Уравнения (6.24) означают экспоненциальный рост производительности труда и предложения труда. Предположим также, что С = wL, т. е. вся заработная плата тратится на потребление. Теперь можно преобразовать уравнения модели с учетом равенств:

Преобразуем уравнения (6.22)-(6.27). Имеем:
 где
где
где
![]()
Поэтому динамика переменных в модели Гудвина описывается системой дифференциальных уравнений:

которая формально совпадает с уравнениями классической модели «хищник - жертва». Это значит, что в модели Гудвина тоже возникают колебания фазовых переменных. Механизм колебательной динамики заключается здесь в следующем: при малой заработной плате w потребление низкое, инвестиции большие, и это приводит к росту производства и занятости у. Большая занятость у вызывает рост средней заработной платы w, что приводит к росту потребления и снижению инвестиций, падению производства и снижению занятости у.
Ниже гипотеза о зависимости ставки процента от уровня занятости рассмотренной модели используется при моделировании динамики однопродуктовой фирмы. Оказывается, что в этом случае при некоторых дополнительных допущениях модель фирмы обладает свойством цикличности рассмотренной выше модели «хищник - жертва».
- См.: Вольтерра В. Указ, соч.; Ризнииенко Г. Ю., Рубин А. Б. Указ. соч.
- См.: Занг В.-Б. Синергетическая экономика. М., 2000.
- См.: Пу Т. Нелинейная экономическая динамика. Ижевск, 2000; Тихонов А. Н.Математическая модель // Математическая энциклопедия. Т. 3. М., 1982. С. 574, 575.
Часто представители одного вида (популяции) питаются представителями другого вида.
Модель Лотки – Вольтерры – модель взаимного существования двух популяций типа «хищник – жертва».
Впервые модель «хищник – жертва» была получена А. Лоткой в 1925 году, который использовал ее для описания динамики взаимодействующих биологических популяций. В 1926 году независимо от Лотки аналогичные (к тому же более сложные) модели были разработаны итальянским математиком В. Вольтерра, глубокие исследования которого в области экологических проблем заложили фундамент математической теории биологических сообществ или т. н. математической экологии.
В математической форме предложенная система уравнений имеет вид:
где x – количество жертв, y – количество хищников, t – время, α, β, γ, δ – коэффициенты, которые отражают взаимодействия между популяциями.
Постановка задачи
Рассмотрим закрытое пространство, в котором существуют две популяции – травоядные («жертвы») и хищники. Считается, что животных не ввозят и не вывозят и что еды для травоядных животных достаточно. Тогда уравнение изменения числа жертв (только жертв) примет вид:
где $α$ – коэффициент рождаемости жертв,
$x$– размер популяции жертв,
$\frac{dx}{dt}$ – скорость прироста популяции жертв.
Когда хищники не охотятся, они могут вымирать, значит, уравнение для количества хищников (только хищников) примет вид:
Где $γ$ – коэффициент убыли хищников,
$y$ – размер популяции хищников,
$\frac{dy}{dt}$ – скорость прироста популяции хищников.
При встрече хищников и жертв (частота встреч прямо пропорциональна произведению) хищники уничтожают жертв с коэффициентом, сытые хищники могут воспроизводить потомство с коэффициентом. Таким образом, система уравнений модели примет вид:
Решение задачи
Построим математическую модель совместного существования двух биологических популяций типа «хищник – жертва».
Пусть две биологические популяции совместно обитают в изолированной среде. Среда является стационарной и обеспечивает в неограниченном количестве всем необходимым для жизни один из видов – жертвы. Другой вид – хищник – также обитает в стационарных условиях, но питается только жертвами. В роли хищников могут выступать коты, волки, щуки, лисы, а в роли жертв – куры, зайцы, караси, мыши соответственно.
Для определенности рассмотрим в роли хищников – котов, а в роли жертв – кур.
Итак, куры и коты живут в некотором изолированном пространстве – хозяйственном дворе. Среда предоставляет курам питание в неограниченном количестве, а коты питаются только курами. Обозначим через
$х$ – количество кур,
$у$ – количество котов.
Со временем количество кур и котов меняется, но будем считать $х$ и $у$ непрерывными функциями от времени t. Назовем пару чисел $х, у)$ состоянием модели.
Найдем каким образом изменяется состояние модели $(х, у).$
Рассмотрим $\frac{dx}{dt}$ – скорость изменения количества кур.
Если котов нет, то количество кур возрастает и тем быстрее, чем больше кур. Будем считать зависимость линейной:
$\frac{dx}{dt} a_1 x$,
$a_1$ – коэффициент, который зависит только от условий жизни кур, их естественной смертности и рождаемости.
$\frac{dy}{dt}$ – скорость изменения количества котов (если нет кур), зависит от количества котов y.
Если кур нет, то количество котов уменьшается (у них нет пищи) и они вымирают. Будем считать зависимость линейной:
$\frac{dy}{dt} - a_2 y$.
В экосистеме скорость изменения количества каждого вида также будем считать пропорциональным его количеству, но только с коэффициентом, зависящим от количества особей другого вида. Так, для кур этот коэффициент уменьшается с увеличением количества котов, а для котов возрастает с увеличением количества кур. Будем считать зависимость также линейной. Тогда получим систему дифференциальных уравнений:

Данная система уравнений называется моделью Вольтерра-Лотки.
a1, a2, b1, b2 – числовые коэффициенты, которые называют параметрами модели.
Как видно, характер изменения состояния модели (x, y) определяется значениями параметров. Изменяя данные параметры и решая систему уравнений модели, можно исследовать закономерности изменения состояния экологической системы.
С помощью программы MATLAB система уравнений Лотки-Вольтерра решается следующим образом:
На рис. 1 представлено решение системы. В зависимости от начальных условий решения разные, чему отвечают разные цвета траекторий.
На рис. 2 представлены те же решения, но с учетом оси времени t (т.е. наблюдается зависимость от времени).
Здесь в отличие от (3.2.1) знаки (-012) и (+a2i) разные. Как и в случае конкуренции (система уравнений (2.2.1)), начало координат (1) для этой системы является особой точкой типа «неустойчивый узел». Три других возможных стационарных состояния:

Биологический смысл требует положительности величин Х у х 2. Для выражения (3.3.4) это означает, что
В случае, если коэффициент внутривидовой конкуренции хищников а ,22 = 0, условие (3.3.5) приводит к условию ai2
Возможные типы фазовых портретов для системы уравнений (3.3.1) представлены на рис. 3.2 a-в. Изоклины горизонтальных касательных представляют собой прямые
а изоклины вертикальных касательных - прямые
Из рис. 3.2 видно следующее. Система хищник -жертва (3.3.1) может иметь устойчивое положение равновесия, в котором популяция жертв полностью вымерла (х = 0) и остались только хищники (точка 2 на рис. 3.26). Очевидно, такая ситуация может реализоваться лишь в случае, если кроме рассматриваемого вида жертв х хищник Х 2 имеет дополнительные источники питания. Этот факт в модели отражается положительным членом в правой части уравнения для хз. Особые точки (1) и (3) (рис. 3.26) являются неустойчивыми. Вторая возможность - устойчивое стационарное состояние, в котором популяция хищников полностью вымерла и остались одни жертвы - устойчивая точка (3) (рис. 3.2а). Здесь особая точка (1) - также неустойчивый узел.
Наконец, третья возможность - устойчивое сосуществование популяций хищника и жертвы (рис. 3.2 в), стационарные численности которых выражаются формулами (3.3.4). Рассмотрим этот случай подробнее.
Предположим равенство нулю коэффициентов внутривидовой конкуренции (аи = 0, i = 1, 2). Предположим также, что хищники питаются только жертвами вида х и в отсутствие их вымирают со скоростью С2 (в (3.3.5) С2
Проведем подробное исследование этой модели, воспользовавшись обозначениями, наиболее широко принятыми в литературе. Переобо-

Рис. 3.2. Расположение главных изоклин на фазовом портрете вольтерров- ской системы хищник жертва при разном соотношении параметров: а - о» б -
С I С2 С2
1, 3 - неустойчивые, 2 - устойчивая особая точка; в -
1, 2, 3 - неустойчивые, 4 - устойчивая особая точка значим
Система хищник-жертва в этих обозначениях имеет вид:

Свойства решений системы (3.3.6) будем исследовать на фазовой плоскости N
1
ON
2
Система имеет два стационарных решения. Их легко определить, приравняв нулю правые части системы. Получим:

Отсюда стационарные решения:

Рассмотрим подробнее второе решение. Найдем первый интеграл системы (3.3.6), не содержащий t. Умножим первое уравнение на -72, второе - на -71 и результаты сложим. Получим:
Теперь разделим первое уравнение на N и умножим на € 2, а второе разделим на JV 2 и умножим на е. Результаты снова сложим:
Сравнивая (3.3.7) и (3.3.8), будем иметь:

Интегрируя, получим:

Это и есть искомый первый интеграл. Таким образом, система (3.3.6) является консервативной, поскольку имеет первый интеграл движения, величину, представляющую собой функцию переменных системы N и N 2 и не зависящую от времени. Это свойство позволяет конструировать для вольтерровских систем систему понятий, аналогичную статистической механике (см. гл. 5), где существенную роль играет величина энергии системы, неизменная во времени.
При каждом фиксированном с > 0 (что соответствует определенным начальным данным) интегралу соответствует определенная траектория на плоскости N 1 ON 2 , служащая траекторией системы (3.3.6).
Рассмотрим графический способ построения траектории, предложенный самим Вольтерра. Заметим, что правая часть формулы (3.3.9) зависит только от Д г 2, а левая - только от N. Обозначим
Из (3.3.9) следует, что между X и Y имеется пропорциональная зависимость
На рис. 3.3 изображены первые квадранты четырех систем координат XOY, NOY , N 2 OX и Д Г 10N 2 так, чтобы все они имели общее начало координат.
В левом верхнем углу (квадрант NOY) построен график функции (3.3.8), в правом нижнем (квадрант N 2 OX) - график функции Y. Первая функция имеет min при Ni = а вторая - max при N 2 = ?-
Наконец, в квадранте XOY построим прямую (3.3.12) для некоторого фиксированного С.
Отметим точку N на оси ON . Этой точке соответствует определенное значение Y(N 1), которое легко найти, проведя перпендикуляр

Рис. 3.3.
через N до пересечения с кривой (3.3.10) (см. рис. 3.3). В свою очередь, значению К(Д^) соответствует некоторая точка М на прямой Y = сХ и, следовательно, некоторое значение X(N) = Y(N)/c, которое можно найти, проведя перпендикуляры AM и MD. Найденному значению (эта точка отмечена на рисунке буквой D) соответствуют две точки Р и G на кривой (3.3.11). По этим точкам, проводя перпендикуляры, найдем сразу две точки Е" и Е ", лежащие на кривой (3.3.9). Их координаты:

Проводя перпендикуляр AM , мы пересекли кривую (3.3.10) еще в одной точке В. Этой точке соответствуют те же Р и Q на кривой (3.3.11) и те же N и Щ. Координату N этой точки можно найти, опустив перпендикуляр из В на ось ON. Таким образом, мы получим точки F" и F", также лежащие на кривой (3.3.9).
Исходя из другой точки N, тем же самым образом получим новую четверку точек, лежащих на кривой (3.3.9). Исключение составит точка Ni = ?2/72- Исходя из нее, получим только две точки: К и L. Это будут нижняя и верхняя точки кривой (3.3.9).
Можно исходить не из значений N , а из значений N 2 . Направляясь от N 2 к кривой (3.3.11), поднимаясь затем до прямой У = сХ, а оттуда пересекая кривую (3.3.10), также найдем четыре точки кривой (3.3.9). Исключение составит точка No = ?1/71- Исходя из нее, получим только две точки: G и К. Это будут самая левая и самая правая точки кривой (3.3.9). Задавая разные N и N 2 и получив достаточно много точек, соединив их, приближенно построим кривую (3.3.9).
Из построения видно, что эго замкнутая кривая, содержащая внутри себя точку 12 = (?2/721 ?1/71)» исходящая из определенных начальных данных N ю и N20. Взяв другое значение С, т.е. другие начальные данные, получим другую замкнутую кривую, не пересекающую первую и также содержащую точку (?2/721 ?1/71)1 внутри себя. Таким образом, семейство траекторий (3.3.9) есть семейство замкнутых линий, окружающих точку 12 (см. рис. 3.3). Исследуем тип устойчивости этой особой точки, воспользовавшись методом Ляпунова.
Так как все параметры е 1, ?2, 71,72 положительны, точка (N[расположена в положительном квадранте фазовой плоскости. Линеаризация системы вблизи этой точки дает:

Здесь n(t) и 7i2(N1, N 2 :
Характеристическое уравнение системы (3.3.13):

Корни этого уравнения чисто мнимые:

Таким образом, исследование системы показывает, что траектории вблизи особой точки представлены концентрическими эллипсами, а сама особая точка - центр (рис. 3.4). Рассматриваемая модель Вольтерра и вдали от особой точки имеет замкнутые траектории, хотя форма этих траекторий уже отличается от эллипсоидальной. Поведение переменных Ni, N 2 во времени показано на рис. 3.5.

Рис. 3.4.

Рис. 3.5. Зависимость численности жертвы N i и хищника N 2 от времени
Особая точка типа центр устойчива, но не асимптотически. Покажем на данном примере, в чем это заключается. Пусть колебания Ni(t) и ЛГгМ происходят таким образом, что изображающая точка движется по фазовой плоскости по траектории 1 (см. рис. 3.4). В момент, когда точка находится в положении М, в систему извне добавляется некоторое количество особей N 2, такое, что изображающая точка переходит скачком из точки М в точку Л/". После этого, если система снова предоставлена самой себе, колебания Ni и N 2 уже будут происходить с большими амплитудами, чем прежде, и изображающая точка двигается по траектории 2. Это и означает, что колебания в системе неустойчивы: они навсегда изменяют свои характеристики при внешнем воздействии. В дальнейшем мы рассмотрим модели, описывающие устойчивые колебательные режимы, и покажем, что на фазовой плоскости такие асимптотические устойчивые периодические движения изображаются при помощи предельных циклов.
На рис. 3.6 изображены экспериментальные кривые - колебания численности пушных зверей в Канаде (по данным компании Гудзонова залива). Эти кривые построены на основании данных по числу заготовленных шкурок. Периоды колебаний численности зайцев (жертв) и рысей (хищников) примерно одинаковы и порядка 9 10 лет. При этом максимум численности зайцев опережает, как правило, максимум численности рысей на один год.
Форма этих экспериментальных кривых значительно менее правильная, чем теоретических. Однако в данном случае достаточно того, что модель обеспечивает совпадение наиболее существенных характеристик теоретических и экспериментальных кривых, г.е. величин амплитуды и сдвига фаз между колебаниями численностей хищников и жертв. Гораздо более серьезным недостатком модели Вольтерра является неустойчивость решений системы уравнений. Действительно, как уже говорилось выше, любое случайное изменение численности того или другого вида должно привести, следуя модели, к изменению амплитуды колебаний обоих видов. Естественно, что в природных условиях животные подвергаются бесчисленному количеству таких случайных воздействий. Как видно из экспериментальных кривых, амплитуда колебаний численностей видов мало изменяется от года к году.
Модель Вольтерра - эталонная (базовая) для математической экологии в той же мере, в какой модель гармонического осциллятора является базовой для классической и квантовой механики. При помощи этой модели на основе очень упрощенных представлений о характере закономерностей, описывающих поведение системы, сугубо математи-
Глава 3

Рис. 3.6. Кинетические кривые численности пушных зверей по данным пуш ной компании Гудзонова залива (Сетон-Томсон, 1987) ческими средствами было выведено заключение о качественном характере поведения такой системы - о наличии в такой системе колебаний численности популяции. Без построения математической модели и ее использования такой вывод был бы невозможен.
В рассмотренном нами выше самом простом виде системе Воль- терра присущи два принципиальных и взаимосвязанных недостатка. Их «устранению» посвящена обширная эколого-математическая литература. Во-первых, включение в модель любых, сколь угодно малых, дополнительных факторов качественным образом меняет поведение системы. Второй «биологический» недостаток модели заключается в том, что в нее не включены принципиальные свойства, присущие любой паре взаимодействующих по принципу хищник-жертва популяций: эффект насыщения хищника, ограниченность ресурсов хищника и жертвы даже при избытке жертвы, возможность минимальной численности жертв, доступных для хищника, и пр.
С целью устранения этих недостатков были предложены разными авторами различные модификации системы Вольтерра. Наиболее ин- тересные из них будут рассмотрены в разделе 3.5. Здесь остановимся лишь на модели, учитывающей самоограничения в росте обеих популяций. На примере этой модели наглядно видно, как может меняться характер решений при изменении параметров системы.
Итак, рассматривается система

Система (3.3.15) отличается от ранее рассмотренной системы (3.3.6) наличием в правых частях уравнений членов вида -7uNf,
Эти члены отражают тот факт, что численность популяции жертв не может расти до бесконечности даже в отсутствие хищников в силу ограниченности пищевых ресурсов, ограниченности ареала существования. Такие же «самоограничения» накладываются и на популяцию хищников.
Для нахождения стационарных численностей видов iVi и N 2 приравняем к нулю правые части уравнений системы (3.3.15). Решения с нулевыми значениями численностей хищников или жертв не будут нас сейчас интересовать. Поэтому рассмотрим систему алгебраических
уравнений
 Ее решение
Ее решение
дает нам координаты особой точки. На параметры системы здесь следует положить условие положительности стационарных численностей: N > 0 и N 2 > 0. Корни характеристического уравнения системы, линеаризованной в окрестности особой точки (3.3.16):

Из выражения для характеристических чисел видно, что если выполнено условие
то численности хищников и жертв совершают во времени затухающие колебания, система имеет ненулевую особую точку устойчивый фокус. Фазовый портрет такой системы изображен на рис. 3.7 а.
Допустим, что параметры в неравенстве (3.3.17) так изменяют свои значения, что условие (3.3.17) обращается в равенство. Тогда характеристические числа системы (3.3.15) равны, а ее особая точка будет лежать на границе между областями устойчивых фокусов и узлов. При изменении знака неравенства (3.3.17) на обратный особая точка становится устойчивым узлом. Фазовый портрет системы для этот случая представлен на рис. 3.76.
Как и в случае одной популяции, для модели (3.3.6) можно разработать стохастическую модель, но для нее нельзя получить решение в явном виде. Поэтому мы ограничимся общими рассуждениями. Допустим, например, что точка равновесия находится на некотором расстоянии от каждой из осей. Тогда для фазовых траекторий, на которых значения JVj, N 2 остаются достаточно большими, вполне удовлетворительной будет детерминистическая модель. Но если в некоторой точке


Рис. 3.7. Фазовый портрет системы (3.3.15): а - при выполнении соотношения (3.3.17) между параметрами; б - при выполнении обратного соотношения между параметрами
фазовой траектории какая-либо переменная не очень велика, то существенное значение могут приобрести случайные флуктуации. Они приводят к тому, что изображающая точка переместится на одну из осей, что означает вымирание соответствующего вида. Таким образом, стохастическая модель оказывается неустойчивой, так как стохастический «дрейф» рано или поздно приводит к вымиранию одного из видов. В такого рода модели хищник в конечном счете вымирает, это может произойти либо случайно, либо вследствие того, что сначала элиминируется популяция его жертвы. Стохастическая модель системы хищник- жертва хорошо объясняет эксперименты Гаузе (Гаузе, 1934; 2000), в которых инфузория Paramettum candatum служила жертвой для другой инфузории Didinium nasatum - хищника. Ожидавшиеся согласно детерминистическим уравнениям (3.3.6) равновесные численности в этих экспериментах составляли примерно всего но пять особей каждого вида, так что нет ничего удивительного в том, что в каждом повторном эксперименте довольно быстро вымирали либо хищники, либо жертвы (а за ними и хищники).
Итак, анализ вольтерровских моделей взаимодействия видов показывает, что, несмотря на большое разнообразие типов поведения таких систем, незатухающих колебаний численности в модели конкурирующих видов не может быть вовсе. В модели хищник жертва незатухающие колебания появляются вследствие выбора специальной формы уравнений модели (3.3.6). При этом модель становится негрубой, что свидетельствует об отсутствии в такой системе механизмов, стремящихся сохранить ее состояние. Однако в природе и эксперименте такие колебания наблюдаются. Необходимость их теоретического объяснения послужила одной из причин для формулировки модельных описаний в более общем виде. Рассмотрению таких обобщенных моделей посвящен раздел 3.5.
